sin(θπ/2)=cosθ は、暗記できるならしても良いですが、 加法定理でいつでも導けるので、忘れても大丈夫と私は思っています。 sin(θπ/2)=sinθcos(π/2) cosθsin(π/2) = sinθ*0 cosθ*1 = cosθ 今回の問題は、以下の方法で解いてみました。(sinθとcosθの関係から出せることを忘れていたので) sin を cosにしIn this video we will learn how to prove sin(π/2 θ) = cos θAlternative method is given in this videohttps//youtube/473wf0vsKgIThe value of sin θcos θ will be greatest when θ=30∘ θ=45∘ θ=60∘ θ=90∘ Let fx=sin θcos θ=√2sinθπ4But−1≤sinθπ2≤1⇒−√2≤√2sinθπ4≤√2Hence the maximum value o
22届人教新高考数学一轮复习作业第4章第1讲三角函数的基本概念 同角三角函数的基本关系与诱导公式2 Word版带解析 莲山课件
Sin(θ+π/2)=cosθ 証明
Sin(θ+π/2)=cosθ 証明- $$\lim_{ϴ→0}\frac{sinϴ}{ϴ}=1$$ We'll prove this result by using the squeeze theorem and basic geometry, algebra, and trigonometry In a future lesson, we'll learn why this result is important the reason being because knowledge that \(\lim_{ϴ→0}\frac{sinϴ}{ϴ}=1\) is required to find the derivatives of the sin and cosine functionsθ と θ+ ( π /2)の関係 sinθ+cosθとsinθcosθの関係 sinθ+cosθ、sinθcosθとsin^3θ十cos^3θ sinθ-cosθとsinθcosθの関係 sinθ-cosθ、sinθcosθとsin^3θ-cos^3θ 三角関数の相互関係を用いる証明




高等数学微积分 北大版 Pages 1 247 Flip Pdf Download Fliphtml5
This does not hold for all θ and ϕFor example, the righthand side is not defined when θ = π/4 and ϕ = π/2 However, as we shall see later, it does hold for all real numbers θ and ϕ for which both sides of the equation are defined Such an equation is called a trigonometric identity Convention When we are given or asked to establish a trigonometric equation involving variables θθ+π/2の三角関数 ~θ+π/2の公式~ \(\displaystyle\sin (\theta\frac{\pi}{2})=\cos \theta\) \(\displaystyle\cos (\theta\frac{\pi}{2})=\sin \theta \) θ = y x で表される3つの三角比の関数のことを、 三角関数 と言います。 「 sin θ, cos θ, tan θ の分母・分子をド忘れしそう」と感じる方も多いかもしれませんが、これらはその 頭文字 s,c,t の筆記体 のイメージと結びつけると覚えやすくなり
符号にも注意を! では、直角三角形イで (θπ/2)の三角比を考えましょう。 「底辺」と「高さ」が入れ替わっているので、 cos (θπ/2)=sinθ sin (θπ/2)=cosθ tan (θπ/2)=1/tanθ と表せます。 符号の変化にも注意してください。 では、ポイントを使って実際に問題を解いてみましょう。となりますね! ここで sin 2 θ cos 2 θ=1 の公式より ( sinθcosθ ) 2 =1 2sinθcosθ となりますね! 差の2乗=1-2×積 となり和の2乗は積で表せられることがポイントです。 では、ポイントを使って実際に問題を解いていきましょう。 ・sin(90°θ)=cosθ ・cos(90°θ)=sinθ ・tan(90°θ)=1/tanθ が成り立ちます. 「(90°θ)型の三角比の変換公式」は覚えるまでもなく,図を見れば成り立つことはすぐに分かります. この動画では,この「(90°θ)型の三角比の変換公式」の考え方を説明し,具体例
Class9 1 vote 1 answer Let the sin(-θ)=-sinθ、cos(-θ)=cosθなど、図を書けば解る三角関数の公式の丸暗記は、いけません。 三角関数の公式を覚える前にする事はs,c,tの筆記体の書き方を英語の先生に聞く事です。 sin cos tanの覚え方。最近は筆記体を学校で習わないので、この基本のsin cos tanの覚え方を知らない人も多いかThe (π/2θ) formulas are similar to the (π/2θ) formulas except only sine is positive because (π/2θ) ends in the 2nd Quadrant sin(π/2θ) = cosθ cos(π/2θ) = sinθ tan(π/2θ) = cotθ cot(π/2θ) = tanθ Proof The Trigonometric ratios of angle (θ) Thinking of θ as an acute angle, (θ) ends in the 4th Quadrant where only cosine is positive (θ) means starting from




数学测试123 By Mac Xu Issuu



Q Tbn And9gcrzz4 1ds9ppsd8y 0vi 8exu9yrzt2issbxxz9kcs1yppfojoc Usqp Cau
Let n ≥ 2 be a natural number and 0 < θ < π/2 Then ∫ (sinn θ sinθ)^1/n cosθ/(sin^n1θ) dθ is equal to (where C is a constant of integration) asked in Mathematics by Niharika (756k points) jee mains 19;== y= sin (θ−α ) のグラフ == 基本の形 y= sin θ のグラフを描くには、右のような対応表(θの値と y の値を表にしたもの)を作り、求めた座標(θ , y )を結んでいく。 この y= sin θ のグラフは、以下の解説を通じて何度も登場する基本の形なので、しっかりとイメージに刻んでおくことが重要。Sin(θ π 2) = cosθ sin(θ π) = −sinθ sin(θ 2π) = sinθ cos(θ π 2) = −sinθ cos(θ π) = −cosθ cos(θ 2π) = cosθ tan(θ π 2) = −(tanθ)−1 tan(θ π) = tanθ tan(θ 2π) = tanθ Les fonctions sinus et cosinus sont p´eriodiques, de p´eriode 2π La fonction tangente est p´eriodique, de p´eriode π 13 Equations trigonom´etriques´ On a les ´equivalences



The Research Progress Of Topological Properties In Spinor Bose Einstein Condensates



2
sin(θπ/2) = sin((θπ/2)π) = sin(θπ/2) = sin(π/2θ) = cosθ この2式を使って、θ = φπ/2 と置けば、 cosφ = sin(φπ/2) sinφ = cos(φπ/2) それとも、sin, cos をべき級数で定義して、 4式の成立を計算で示して欲しいのか?Sinθcosθ 解説 要点 (解説) 2つの変数 x , y があるときに,それらの和 xy の値が与えられても,それらの積 xy の値は決まらないし,逆にそれらの積 xy の値が与えられても,それらの和 xy の値も決まらない. しかし, sin θ , cos θ の値は, sin 2θ If pi/2≤θ≤π and sin θ =4/5, find the exact value of cosθ and cotθ?
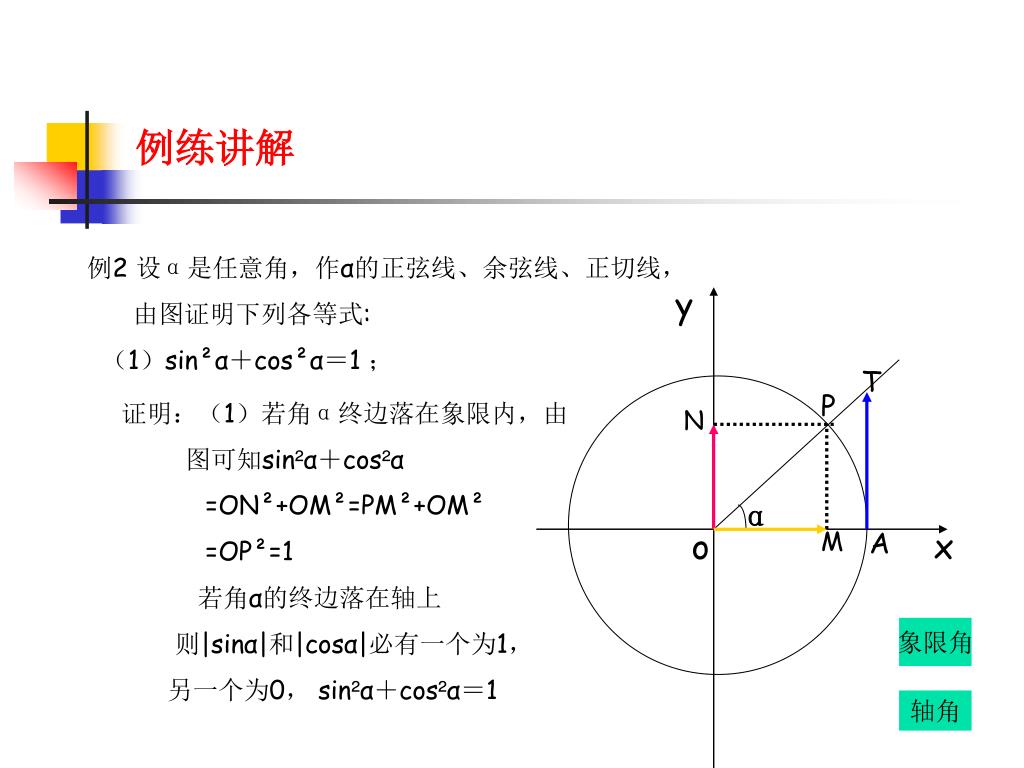



Ppt 1 2 2 单位圆与三角函数线powerpoint Presentation Free Download Id



E1jqn5dfguejvm
高校 オンライン健康相談gooドクター登場 24時間365日いつでも医師に健康相談できる! 詳しくはコチラ>> cos (θπ/2)=sinθ sin (θπ/2)=cosθ になるんですか? 数学 sin (θ+2分の3π)が (θ+2分のπ)+πになって −sin (θ+2分のπ)になって 結果 − 英語 Find the slope of the normal to the curve x = 1 − a sin θ, y = b cos^2θ at θ=π/2 asked in Mathematics by sforrest072 (128k points) application of derivative;1 < θ/sinθ < 1/cosθ θ→0の時、右辺の極限は1だから、「はさみうちの原理」より、中央の θ/sinθの極限も1となる。したがって、(sinθ)/θの極限も1。 一方、 -π/2<θ<0 の場合は、θ=-t とおけば上と同様。 結局、いずれにせよ、lim (sinθ)/θ = 1 (θ→0)。 (Q.E.D.証明



Http Lsec Cc Ac Cn Liuxin Calculus Calculus Lx 14 Pdf



Http Zhuhx Net Lectures Complexanalysis Week2 Pdf
Cos (θ+π)=−cosθ tan (θ+π)=tanθ の公式を利用して、次の公式を証明してみましょう。 sin (π−θ)=sinθ cos (π−θ)=−cosθ tan (π−θ)=−tanθ 公式の証明は 加法定理 を用いておこなうこともできますが、今回は加法定理を学習していなくてもできるSin(90 θ)=cosθ 証明 b,簡単に導くことができます. 探究三角恆等式(1) tanθ = sinθ/cosθ(2) sin2 θ cos2 θ = 1(3) sin(90 −θ) = cosθ(4) cos(90 −θ) = sinθ(5) tan(90 −θ) = 1/tanθ 上載者 更新日期 版權聲明 版權聲明 教材由教育局提供。0 votes 1 answer Let α and β be the roots of the quadratic equation x^2 sinθ– x(sinθcosθ 1) cosθ = 0 (0 < θ< 45º), and α < β asked Apr



为什么数学与自然科学中许多公式 定理 定律会与p 有联系 知乎




Show That Sin Pi 2 X Cos X Youtube
Solution Solve for θ in the following equation sin 2θ = cosθ Prev Article Next Article (Last Updated On ) Problem Statement ECE Board April 1993 Solve for θ in the following equation sin 2θ = cosθ A 30° B 45° C 60° D 15° Problem Answer θ is equal to 30° View Solution Latest Problem Solving in Plane Trigonometry Problems More Questions in Plane0 votes 1 answer If tan ( π/4 θ) tan (π /4 − θ) = p sec 2θ, then find the value of p asked in Trigonometry by Gaangi (248k points) trigonometry; Prove that y = 4sinθ/(2 cosθ) θ is an a increasing function of θ in 0, π /2 Prove that the function f given by f (x) = log sin x is strictly increasing on (0, π/2) asked in Derivatives by Beepin (587k points) application of derivative;



Http Web Math Sinica Edu Tw Math Media D263 Pdf
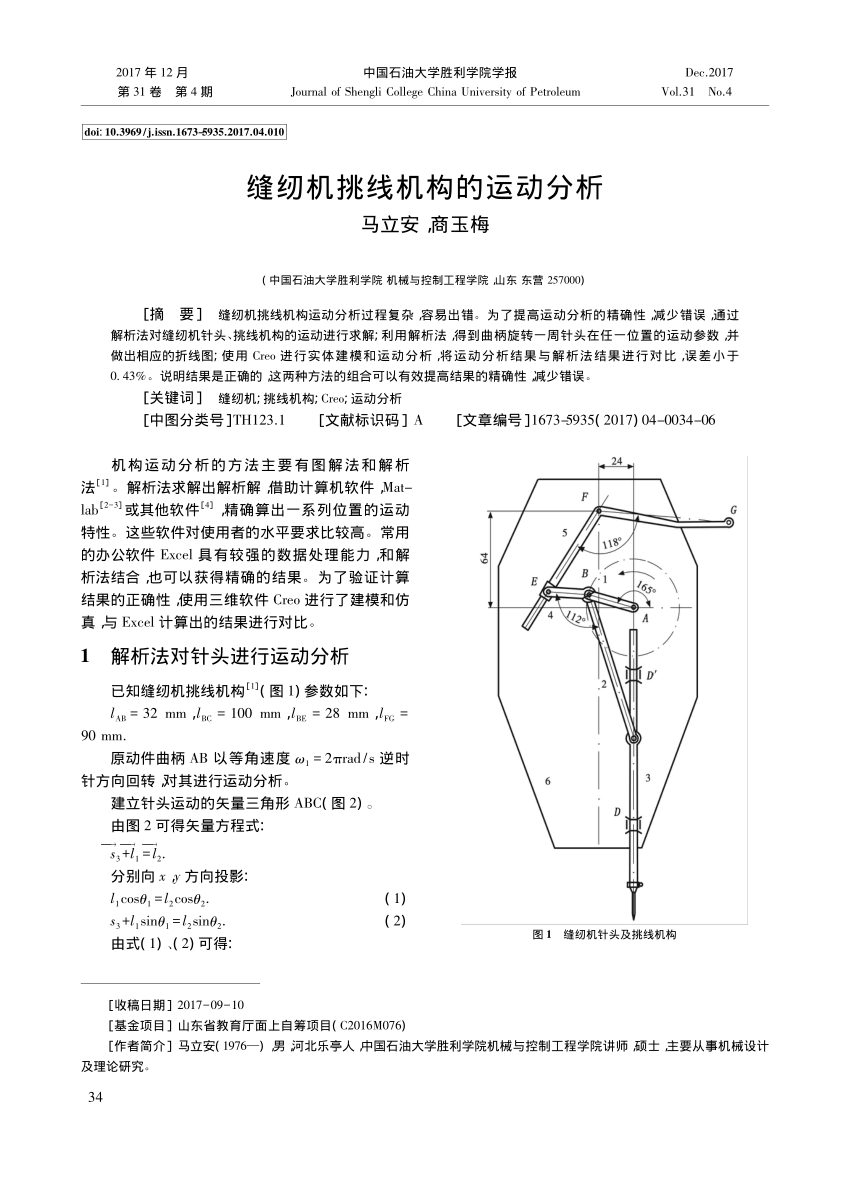



Pdf 缝纫机挑线机构的运动分析
θ+π/2の三角関数の公式 次の公式を証明していきます。 図のように座標上に POAをとり、∠POA=θ、OP=1とします。 POAを、原点中心に"π/2"だけ回転させた三角形を QOBとします。 イメージしにくい人は、"π/2"を度数法で考えてみてください。 "π/2"は、度数法では"90°"です。 つまり POAを90°回転させた三角形を QOBとする ということです。 " ∠QOA=θ+π/2 "であるπ/2−θの三角関数の公式 これらの公式を利用して、次の公式を証明してみましょう。 公式の証明は加法定理を用いておこなうこともできますが、今回は加法定理を学習していなくてもできる方法で行います。 sin(π/2−θ)=cosθ角度がθの直角三角形を図に示し、θπがどの位置に移るのか考えてみましょう。 角度θの直角三角形アが第1象限にあったとします。 θπということは、ここから更に π=180° 移動した場所に直角三角形が来ることを表しています。 第3象限 に移動してイの三角形になりますね。 このイの直角三角形に注目しましょう。 cos (θ+π)の値は 底辺/斜辺 で, アの直角三角形




电子电路大全



Signals And Systems With Python
sin 2 θ cos 2 θ = 1 \sin^2\theta\cos^2\theta=1 sin 2 θ cos 2 θ = 1 の証明です。 sin θ, cos θ \sin\theta,\cos\theta sin θ, cos θ の定義は sin θ = B C A C \sin\theta=\dfrac{BC}{AC} sin θ = A C BC , cos θ = A B A C \cos\theta=\dfrac{AB}{AC} cos θ = A C A B であった。 よって,I tried doing this problem but got stuck midway through I need some help finishing this problem 三角関数の定積分を複素積分で行う(その1) を計算することによって、求めることができる。 ∮ Cg (z)dzを計算する。 と計算できる。 そこで、留数を求めよう。 となって、証明できた。 ∫ 0→π1/ (2sinθ) dθ だったらどうだろうか? 通常の解法は



Influence Of Bias Magnetic Field Direction On Band Structure Of Magnetic Photonic Crystal And Its Role In Constructing Topological Edge States



R 3cos8r 1 Cos8 万图壁纸网
19/7/27 1954 基礎公式の sin(90°θ)=sin (π/2θ)=cosθ もしくは sin (θ90°)=sin (θπ/2)=cosθ を利用するために変形が必要です。 どちらでもよいですが、この例題は前者を用いていますね sin (θπ/2)=sin{π (π/2θ)}は、おっしゃる通り公式を利用するため、 π/2を、ππ/2に変形しています。 sin (θπ/2)=sin (π/2θ)となるのは、 途中、加法定理が使われていると考えるWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get



餘弦 维基百科 自由的百科全书



48s96ub7b0z5f Net Sankakukansuu Seishitsu



纳米金刚石氮空位中心耦合机械振子的纠缠动力学特性



Ppt 1 2 2 单位圆与三角函数线powerpoint Presentation Free Download Id




Worked Example Derivatives Of Sin X And Cos X Video Khan Academy



2cos8 万图壁纸网




高中数学1 2 2 同角三角函数的基本关系课件新人教a版必修4 Ppt课件




17学年高中数学人教a版必修4教材习题点拨 三角函数 莲山文库



Identifying Two Different Configurations Of The Begin Document End Document By The Direct Above Threshold Ionization Spectrum In Two Color Laser Field



第2 章三角学回顾 Manbetx社区




青岛版数学1一6年级下册第7单元测试卷一 含答案 可下载



Opencv学习霍夫直线houghlines和houghlinesp Obsorb Knowledge的博客 Csdn博客




青岛版数学1一6年级下册第7单元测试卷一 含答案 可下载




高一数学复习练习题 1




为什么数学与自然科学中许多公式 定理 定律会与p 有联系 知乎



1




12堂魔力数学课 第9章用途多多的三角学 在线免费阅读 鬼书集




证明三角形中三角满足cota 2 Cotb 2 Cotc 2 Cota 2cotb 2cotc 2 Qixiang Chen的博客 Csdn博客




Pdf Limit Cycles For A Class Of Discontinuous Planar Quadratic Differential System



Polarization Regulation Characteristics Of Reflected Waves At The Interface Of Double Topological Insulators




この問題はsin 8 P 2 Cos8 Clear




2倍角の公式と半角の公式 おいしい数学



Generation Of Surface Plasmon Vortices Based On Double Layer Archimedes Spirals



经典实用 12届高三数学第一轮总复习第4单元课件文新课标人教b版 图文 百度文库




函数名正弦余弦正切余切正割余割下载 Word模板 爱问共享资料




青岛版数学1一6年级下册第7单元测试卷一 含答案 可下载



2cos8 万图壁纸网



Sin 8 P 2 や90 8など還元公式の覚え方の解説 余角 補角の攻略



已知圆的极坐标方程已知圆的极坐标方程为p 2 4 2pcos 8 P 4 6 0



22届人教新高考数学一轮复习作业第4章第1讲三角函数的基本概念 同角三角函数的基本关系与诱导公式2 Word版带解析 莲山课件



2cos8 1 万图壁纸网



2cos8 1 万图壁纸网




Complex Analysis Show Z N Z N 2cos N Theta Request Youtube



纳米金刚石氮空位中心耦合机械振子的纠缠动力学特性




12年数学一轮复习试题随意率性角和弧度制及随意率性角的三角函数 Doc 文档编号 其他文档 帮帮创意网




Pdf 基于解析均匀化模型的蜂窝夹芯板静力弯曲分析




高中数学三角函数知识点 知乎




第3章三角恒等变换单元练习 苏教版必修4 Doc 文档分享网




Pdf Peeling Property Of Bondi Sachs Metrics For Nonzero Cosmological Constant



2cos8 1 万图壁纸网



正切 快懂百科



S R S Arm Ik Redundancy Warheat Robocup
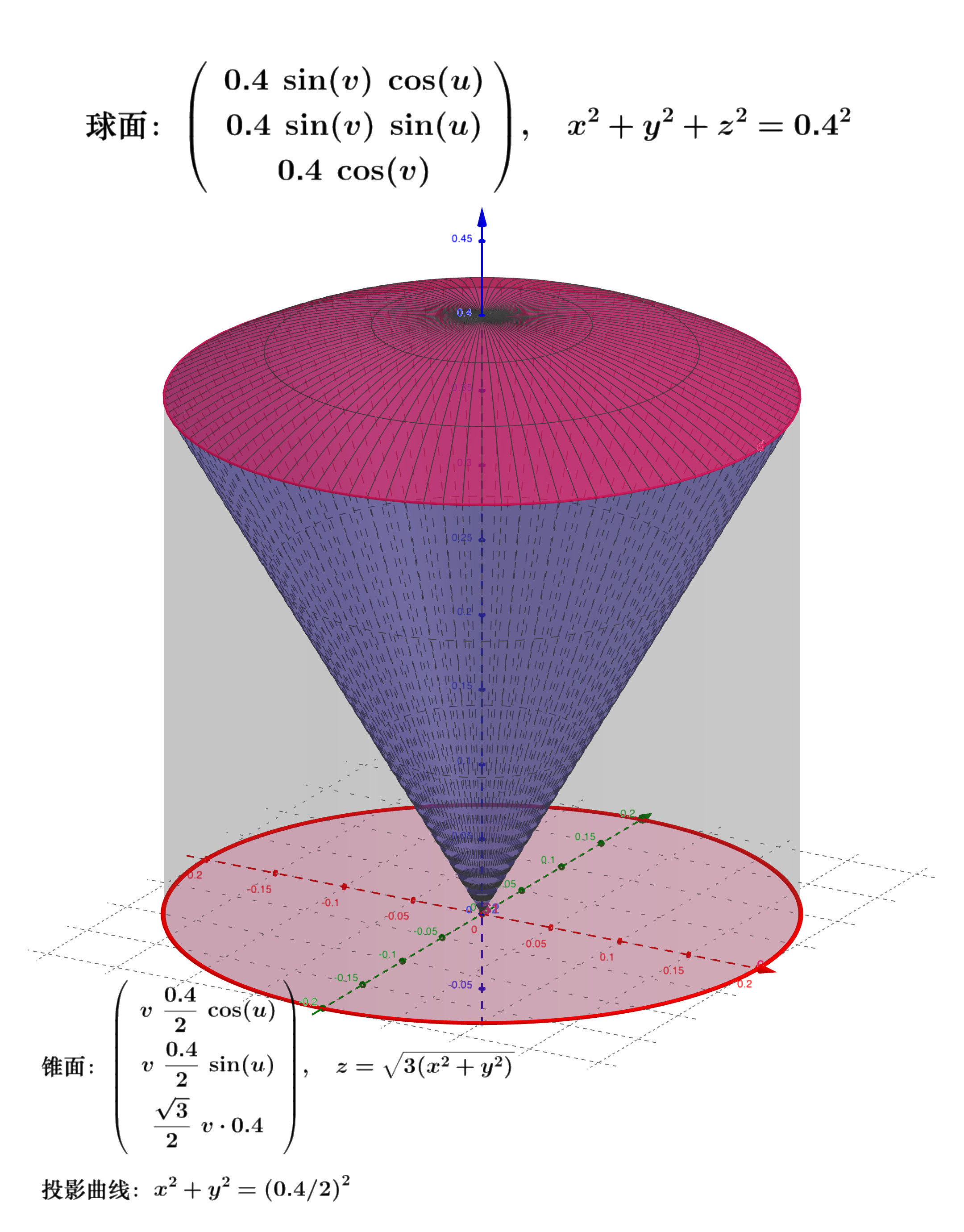



解析几何初步 Guoning Wu Ph D




Gaindaily03 3 19 Palace W的博客 Csdn博客



Linear Neocities Org Chap9 Pdf




Sin 90 8 Cos8 証明第一章 Ocbzpz



Http Zhuhx Net Lectures Complexanalysis Week2 Pdf




06年全国高中数学联赛下载 在线阅读 爱问共享资料




Further Mathematics



3 2 1倍角公式 图文 百度文库




青岛版数学1一6年级下册第7单元测试卷一 含答案 可下载




Prove That Cos Pi Theta Cos Theta Cos Pi Theta Cos Pi 2 Theta Cot Theta Youtube



2



1



Cos P 2 万图壁纸网



2sincos 万图壁纸网



第2 章三角学回顾 Manbetx社区




习题课同角三角函数的基本关系与诱导公式下载 Ppt模板 爱问共享资料



3 2 1倍角公式 图文 百度文库



2
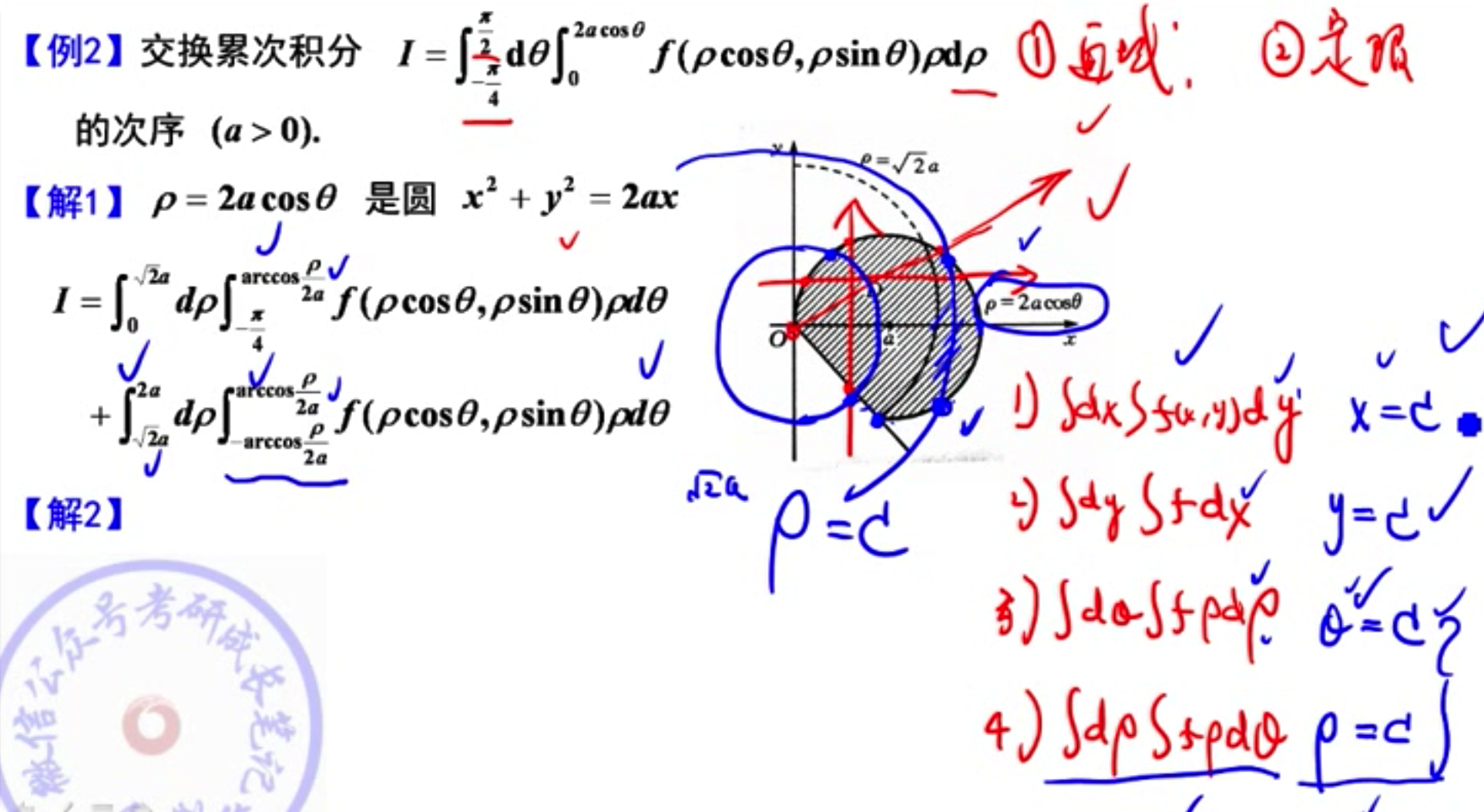



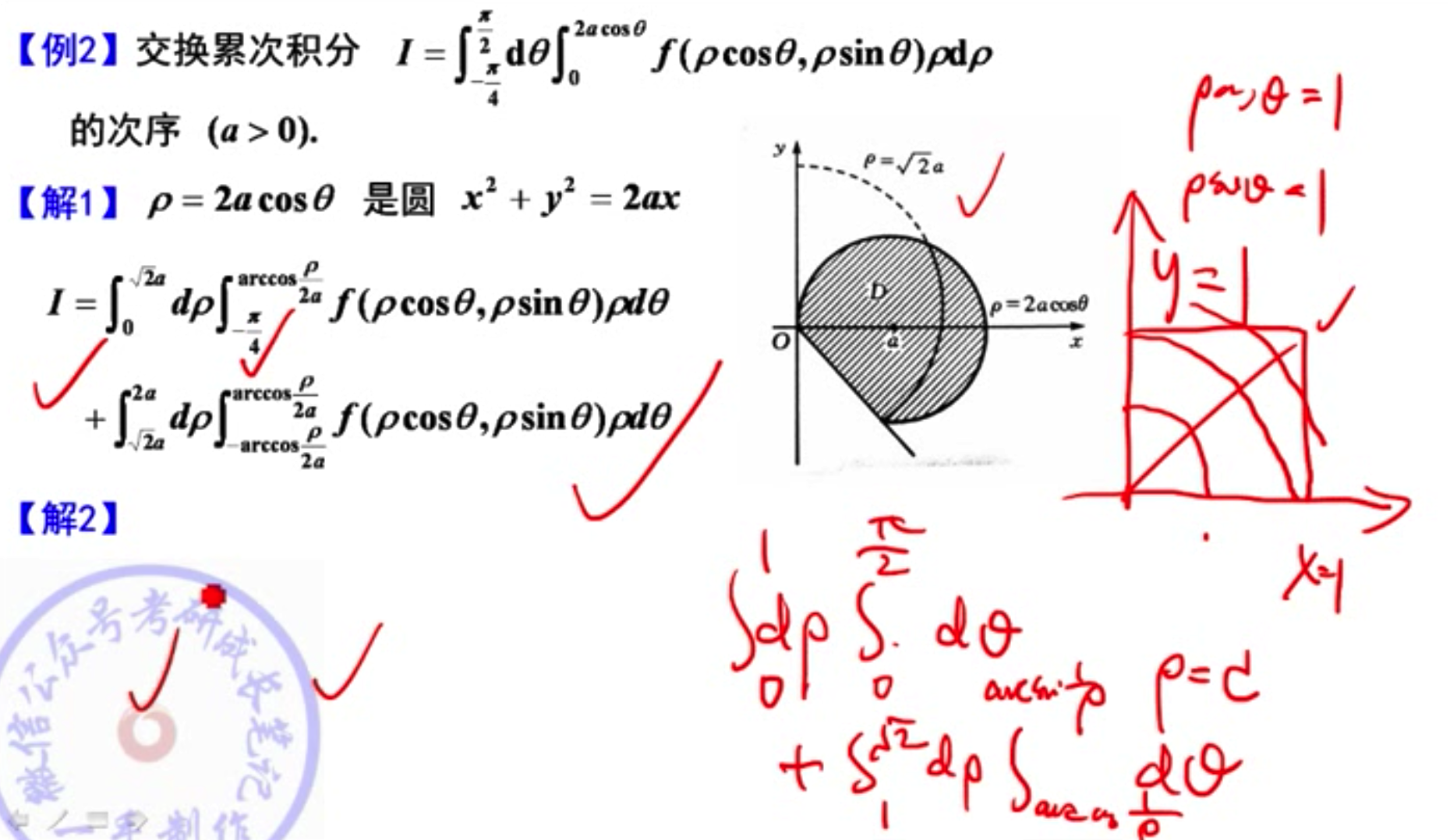
09 二重积分




8 2np 8 8 P 8 P 2 P 8 P 2 8の三角関数 数学ii 三角関数 7 Youtube




Calameo 高中数学公式大全




Prove That Costheta 1 Sintheta Tan Pi 4 Theta 2



正切 快懂百科




17新课标 全国高考文科数学试卷含答案下载 Word模板 爱问共享资料



1




高等数学微积分 北大版 Pages 1 247 Flip Pdf Download Fliphtml5



How Do You Prove Cos X Pi 2 Sin X Socratic
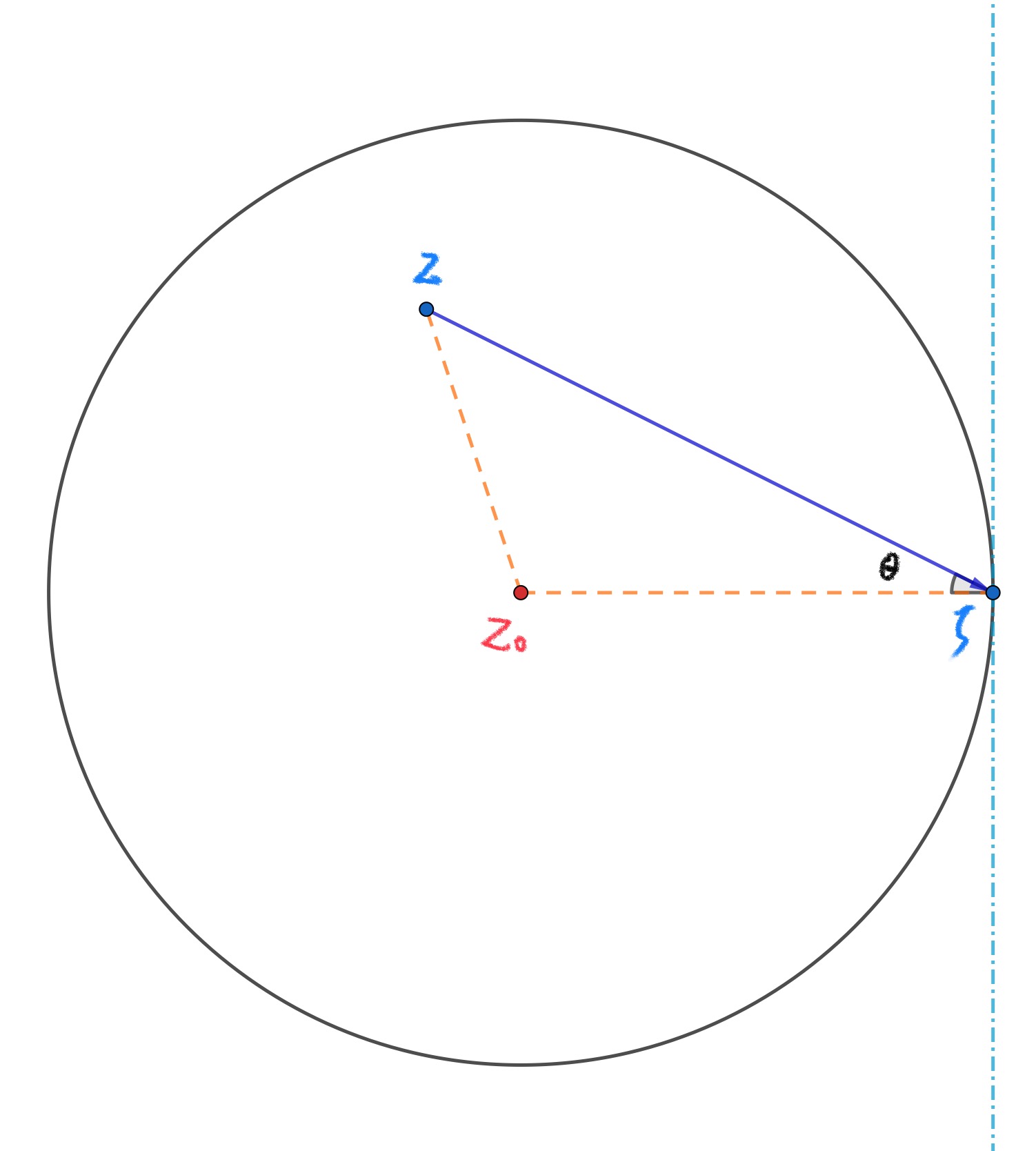



数学分析习题解 一致收敛性 函数项级数与函数族的基本运算 2 虎头微分同学的blog




大一上学期 高等数学 知识整理 第五章定积分及其应用 哔哩哔哩




19 学年新教材高中数学第5章三角函数5 3 诱导公式第2课时诱导公式五 六教 三一刀客
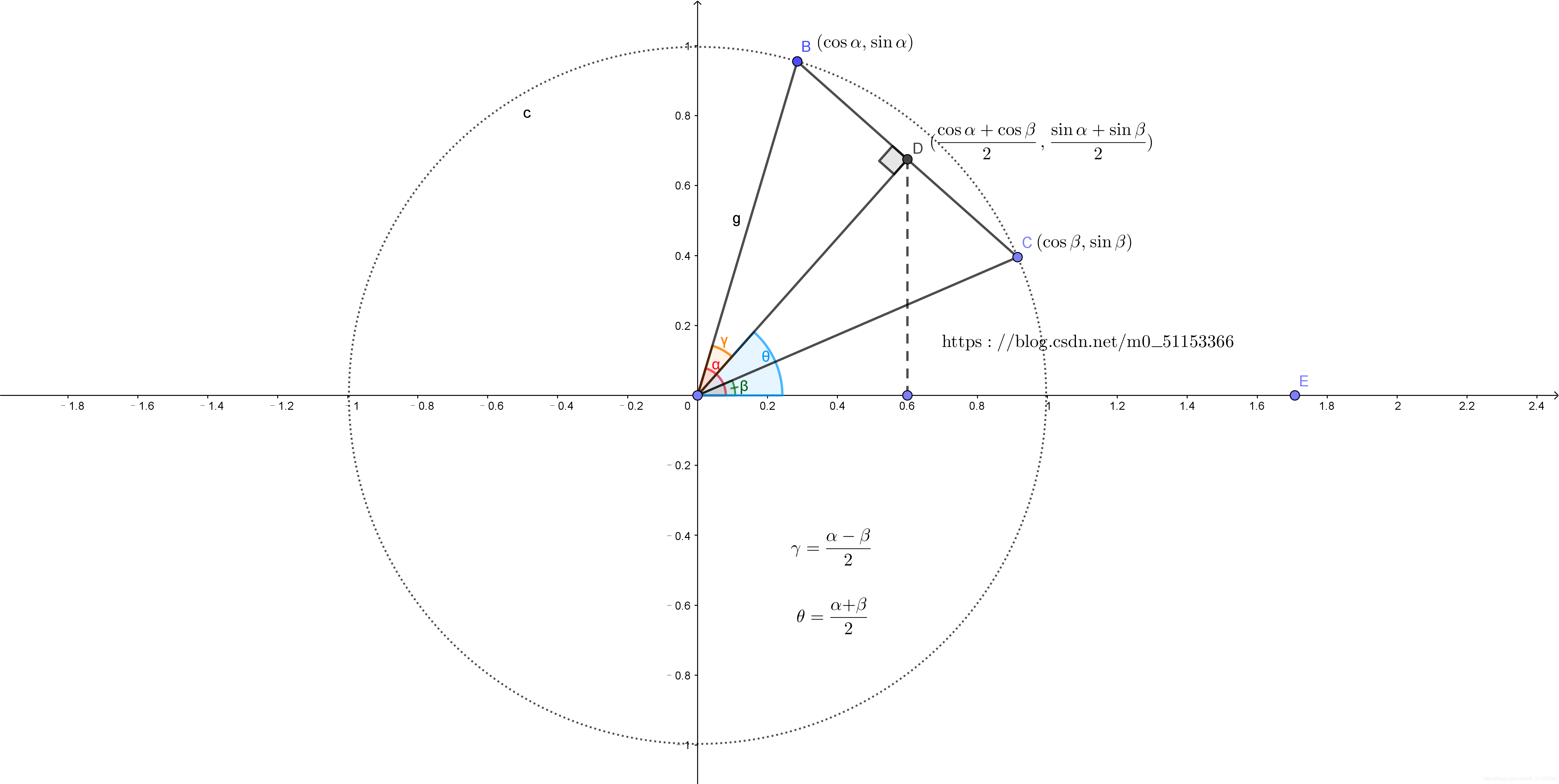



和差化积和积化和差 M0 的博客 Csdn博客




三角函数下载 Word模板 爱问共享资料



Cos0 万图壁纸网




第5章高等数学问题的matlab解法5 1 函数极限和导数本节习题5 2 解析几何和多变量分析5 3 数值积分和微分方程数值解 Ppt Download



Http Zhuhx Net Lectures Complexanalysis Week2 Pdf




Pdf The Simultaneous Approximation Average Errors Of Lagrange Interpolation On The 1 Fold Integrated Wiener Space



第2 章三角学回顾 Manbetx社区



Coupling Mechanism Of Mass Transport And Electrochemical Reaction Within Patterned Anode Of Solid Oxide Fuel Cell




Cabinet 2 Pdf
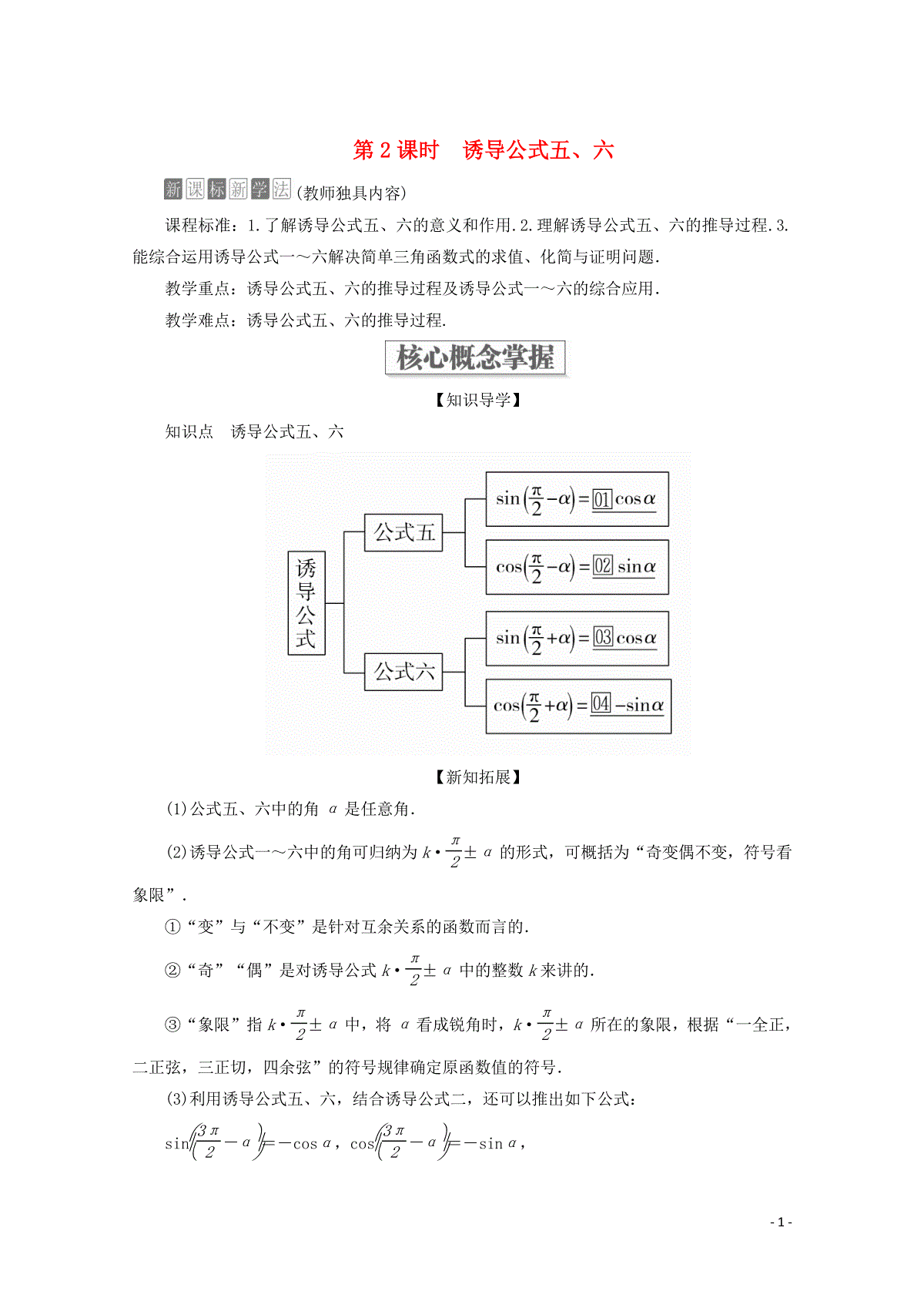



19 学年新教材高中数学第5章三角函数5 3 诱导公式第2课时诱导公式五 六教 三一刀客




1952 1999年全国高考试卷及答案数学pdf版




Ppt 第二节数量积向量积混合积powerpoint Presentation Free Download Id




Sin 90 8 Cos8 証明第一章 Ocbzpz



Nonequilibrium States In Quantum Materials Under Time Period Driving
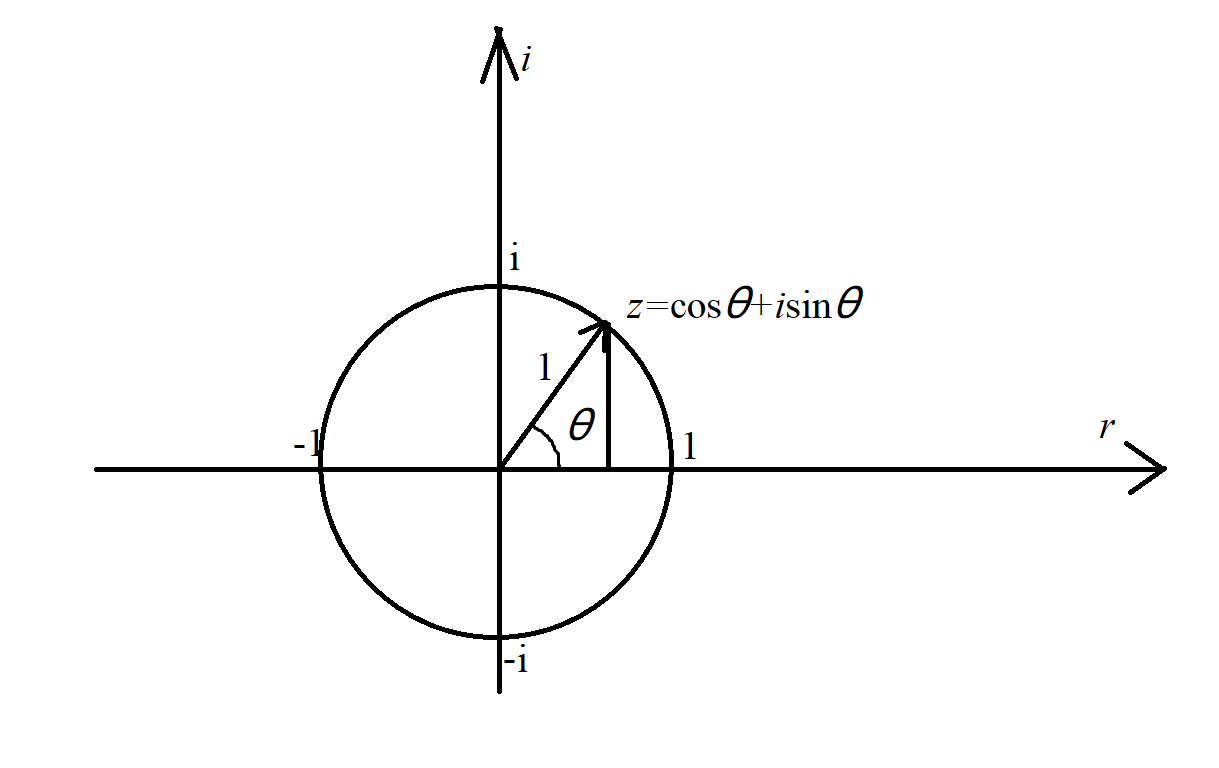



关于单位根和原根 Steven Meng S Blog




青岛版数学1一6年级下册第7单元测试卷一 含答案 可下载


